Cosa succede se matematici e architetti giocano con le bolle di sapone?
Perché la natura preferisce alcune forme? Come mai gli alveari sono composti da tasselli esagonali e non quadrati? E per quale ragione i corpi celesti sono sferici e non a forma di cubo?
Non lo sappiamo. Nel corso della storia però sono stati svelati alcuni principi che permettono di predire quali forme la natura sceglierà in una certa situazione.
Una cosa è certa: le forme della natura sono belle ed efficienti! Non stupisce quindi che da sempre architetti e ingegneri ne traggano ispirazione. Ripercorriamo questa storia… a partire dalle bolle di sapone!

La ricerca della semplicità: ottimizzazione delle forme in natura
Gli antichi greci erano certi che l’ordine e l’armonia presenti nell’universo fossero esprimibili matematicamente. Solo nel XVIII sec. però gli scienziati osarono formulare una legge universale: “Poiché la forma di tutto l’universo è assolutamente perfetta, pensata dal più saggio dei creatori, nel mondo non accade niente senza che si renda evidente una qualche regola di minimo o di massimo” (Eulero).
Il principio di minimo afferma che la natura agisce sempre con la maggiore economia possibile. Un esempio? La luce va da un punto ad un altro scegliendo sempre il percorso più veloce! Nella foto un raggio di luce si fa strada tra le spettacolari forme dell’Antelope Canyon (U.S.A).

Ma perché ci interessano i principi di minimo (e di massimo)?
Questi principi non sono un capriccio, ma hanno grandissima utilità pratica. Ne era convinta la regina Didone! Si racconta che al suo arrivo in Africa, il re Iarba le disse che avrebbe potuto avere tanto terreno quanto poteva abbracciarne una pelle di toro. Il dipinto di Pittoni ritrae la regina mentre indica di tagliare la pelle. Dopo averla ridotta in strisce sottili, le legò tra loro costruendo una corda e con questa formò una circonferenza: il perimetro della sua nuova città, Cartagine. Didone aveva cioè intuito che il cerchio era la figura geometrica che poteva permetterle, a parità di perimetro, di racchiudere l’area più grande!
Ma ognuno di noi ogni giorno si trova a che fare con problemi di ottimizzazione: usiamo il navigatore per percorrere la strada più veloce… o, se ci muoviamo a piedi, quella più breve!

Avete mai giocato con le bolle di sapone?
Le bolle di sapone sono l’esempio visibile del principio di minimo (e di massimo). Come abbiamo detto, la natura è molto efficiente: per questo le bolle di sapone sono sferiche! La sfera infatti è una superficie minima, cioè la superficie più piccola che può racchiudere un volume dato. L’astuta Didone ha sfruttato la forma duale di questa proprietà: la sfera (il cerchio) è la figura che a parità di superficie (perimetro) contiene il volume massimo (l’area massima).
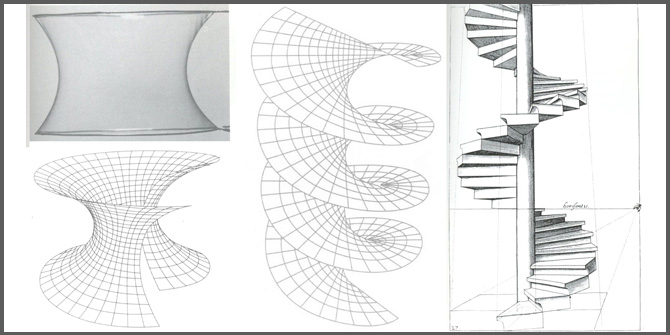
Ora, cosa succede se immergiamo due fili metallici chiusi in una soluzione di sapone e poi li solleviamo? Se siamo fortunati, possiamo vedere una pellicola di sapone connessa, delimitata da ambedue i fili. Ecco a voi il più antico esempio di superficie minima curva, nota ai matematici con il nome di catenoide.
Adesso costruiamo un modello della catenoide, tagliamolo lungo un meridiano e tiriamo con delicatezza le due parti tagliate. Riusciamo a piegare la catenoide senza distorsione e otteniamo un’altra superficie minima: l’elicoide. L’elicoide è stato usato da molti architetti per progettare scale a chiocciola… e da madre natura per costruire la doppia elica del nostro DNA.
Alcuni esempi di ottimizzazione delle forme in architettura
Ai tempi in cui la modellazione computazionale non esisteva, il genio dell’architetto e ingegnere Frei Otto (1925-2015) ha saputo sfruttare le proprietà delle pellicole di sapone per ottenere coperture dalla forma ottimale: strutture leggere ed economiche, concepite per impiegare la minore quantità possibile di materiale.
Otto e i suoi collaboratori usavano fili sottilissimi legati alle estremità di spilli fissati su una lastra di plexiglas. Immergevano queste configurazioni in una soluzione di sapone, ottenendo una pellicola che fa tendere i fili e li unisce con una superficie che minimizza l’area. L’affinamento del progetto avveniva poi mediante modelli solidi, realizzati con sistemi di corde e membrane elastiche, testati in galleria del vento.
Queste spettacolari coperture sfruttano al massimo i materiali impiegati. Le funi di acciaio e le membrane sintetiche lavorano solo in trazione, i pennoni e gli archi di supporto a compressione. Vediamo nelle foto gli studi con pellicole saponose effettuati per l’Istituto di strutture leggere dell’Università di Stoccarda (1964) e lo Stadio olimpico di Monaco (1972).

Anche la forma ideata da Sergio Musmeci per il ponte sul Basento (1976) nasce da studi effettuati con soluzione saponosa. Questa geometria ottimizza il rendimento del materiale, che nel suo caso lavora a compressione, ed è stata affinata mediante prove su modelli elastici in neoprene e modelli rigidi in metacrilato. Questa foto ritrae l’architetto che cammina sulla membrana continua in cemento armato che unisce gli appoggi del ponte.

I modelli “appesi” utilizzati da Antoni Gaudì sono un altro esempio di ricerca della geometria ottimale per strutture che lavorano prevalentemente a compressione. Gaudì sfrutta la forma naturalmente assunta da elementi flessibili (come funi) soggetti alla gravità.
Si dice che l’architetto, chiamato a progettare la chiesa di Santa Coloma nel 1898, abbia suscitato la perplessità dei suoi operai. Entrato in cantiere, appese una tavola con il disegno della pianta della chiesa al soffitto. Sospese dei fili nei punti corrispondenti ai pilastri e agli incroci delle pareti, poi vi appese sacchi pieni di sabbia, proporzionali ai carichi previsti per la struttura. La geometria che ottenne, una volta invertita, corrispondeva alla funicolare del sistema di forze relativo a quella particolare combinazione di carico. Le foto mostrano il modello “rovescio” e lo schizzo di Santa Coloma, mai terminata in questa forma per mancanza di fondi.

“La forma è l’incognita, non le tensioni”
Così Musmeci riassume l’approccio adottato nei modelli fisici che abbiamo visto (pellicole di sapone, modelli elastici e modelli “appesi”). La geometria strutturale non è dato noto, ma è ottenuta esplorando la capacità del materiale di auto-organizzarsi sotto particolari condizioni di carico e vincolo.
Vedremo prossimamente altri metodi di ricerca delle forme ottimali in architettura. Cosa li accomuna? Lo stesso tentativo di “comprendere le forti analogie che è possibile avere con la natura, quindi applicare le conoscenze delle strutture naturali alle strutture della tecnica” (A.Capasso).
IMMAGINI 1: http://acrylico-ariafresca.blogspot.it/2015/07/; 2: http://www.meteoweb.eu/2014/05/viaggio-nella-terra-dei-navajo-alla-scoperta-di-incredibili-formazioni-geologiche-naturali/283183/; 4-5-6: S. Hildebrant e A. Tromba, “Principi di minimo”; 5: https://it.pinterest.com/pin/505810601868794324/; 6: https://it.pinterest.com/pin/526287906433857744/; 7: http://presstletter.com/2013/07/lincognita-della-forma-minima-di-gabriello-grandinetti/; 8: https://it.pinterest.com/pin/428756826995438751/?lp=true; https://it.pinterest.com/pin/428756826995240730/

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
